Code comments as live wikis in IDEs

In this article we explore how code comments can become a live wiki if we rely on interactive notebooks to document our systems directly inside the IDE.

Glamorous Toolkit is the moldable development environment made of multiple programmable and combinable components. One of the components is Documenter, the engine that makes creating and consuming code documentation and tutorials a beautiful experience directly in the IDE. It enables:

- documentation of existing code

- tutorials

- interactive data notebooks

This article explores the use of Documenter for documenting code.

Code comments are pervasive in software development. They are used for many reasons, including, but not limited to, documenting design decisions, explaining what code does, clarifying implementation details, or showing how to use a piece of code.

In spite of their wide usage, code comments can also be problematic. Taking the time to refactor unclear code is sometimes better than explaining what that code does in a comment. Once written a comment needs to be kept up to date as the code changes, especially if documenting usage. Comments are more often than not only textual, limiting what the writer can embed.

In this article we explore how code comments, and the documentation about our software systems, can look like if we treat the IDE as a live wiki. As an example system we use a demo application that detects faces within pictures using the Azure Face API described in another article.

A first class comment

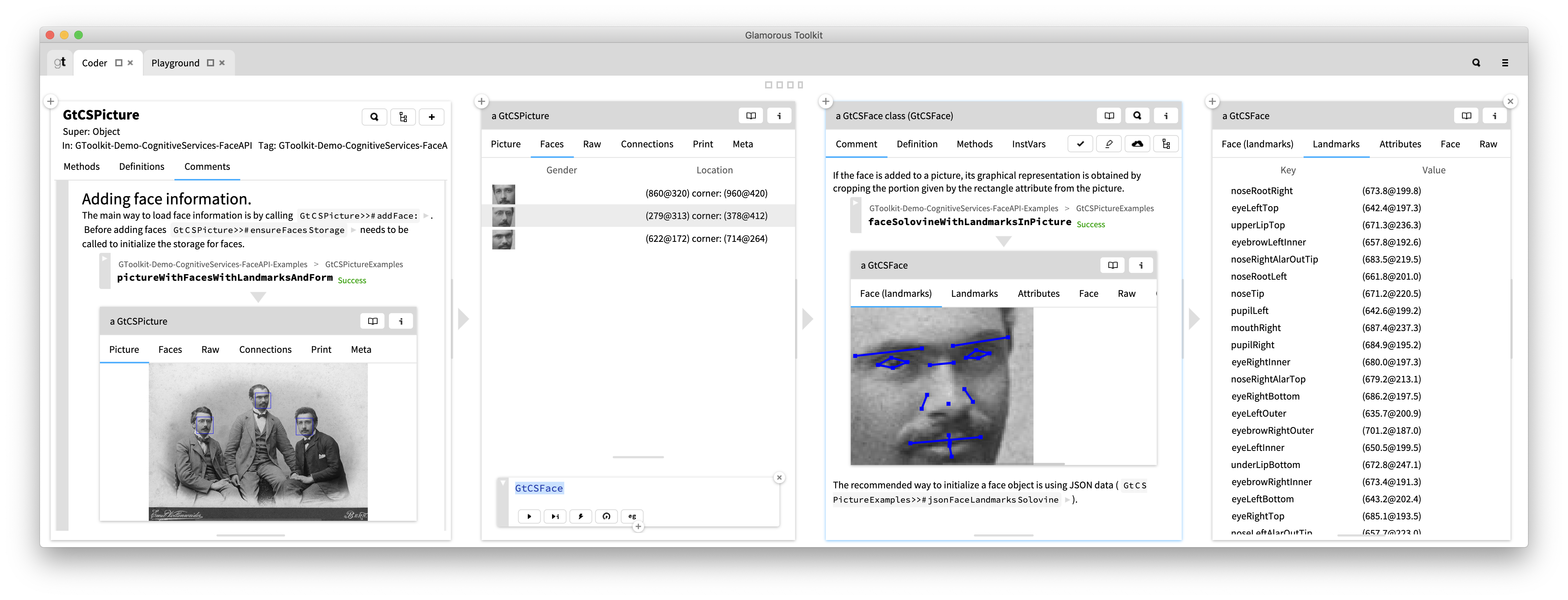
A class from our demo application is the Face class. This class models a face detected within a picture. We could comment this class as follows:

        
I model a face detected in a picture object.

I store the rectangle delimiting the face within a {@link Picture} object, face attributes ({@link FaceAttributes}), and face landmarks ({@link FaceLandmarks}). I also point to the picture object that contains the face.

The rectangle delimiting a face and landmarks can be added to a face, even if the face does not have a graphical representation. If the face is added to a picture, its graphical representation is obtained by cropping the portion given by the rectangle attribute from the picture.

<pre>
 face := GtCSFace new
  rectangle: ((622@172) corner: (714@264)).
 picture := GtCSPicture new.
 picture ensureFacesStorage.
 picture addFace: face.
 picture loadPictureFormFile: PictureExamples class pictureFile.
 picture 
</pre>

The recommended way to initialise a face object is using JSON data ({@link PictureExamples>>#jsonFaceLandmarksSolovine}).

This is just one of many possible comments for this class. Still, it has characteristics often encountered in comments, like links to other code entities, and code snippets to show usage.

Nonetheless, the comment talks about pictures and faces but only shows text; it has a code snippet but often the IDE offers no direct way to execute that code and explore the result; renames of classes and methods often do not take into account code snippets embedded into comments.

This comment also aims to convey details about the structure and behaviour of a class. However, the tools that we use to view comments, more often than not assume that comments are pieces of static text meant only to be read.

A different perspective

Let us explore next a different way to consume this comment.

From snippets to executable examples

An important part of this particular comment is the code snippet. It shows how to create and initialise a Face object. Instead of having just a standalone code snippet embedded only in this comment, we transform the snippet into a standalone example method (a test method that returns an object), and embed in the comment a live editor for interacting with that example.

Code comments can embed code by taking it from example methods, instead of directly holding the code.

This makes it easier to maintain and test the snippet. It also makes it possible to execute it and inspect the returned object directly in the code comment. We do not need to copy-paste code, open another tool, or do any other kind of setup to run this code. Below we execute the example and explore the result.

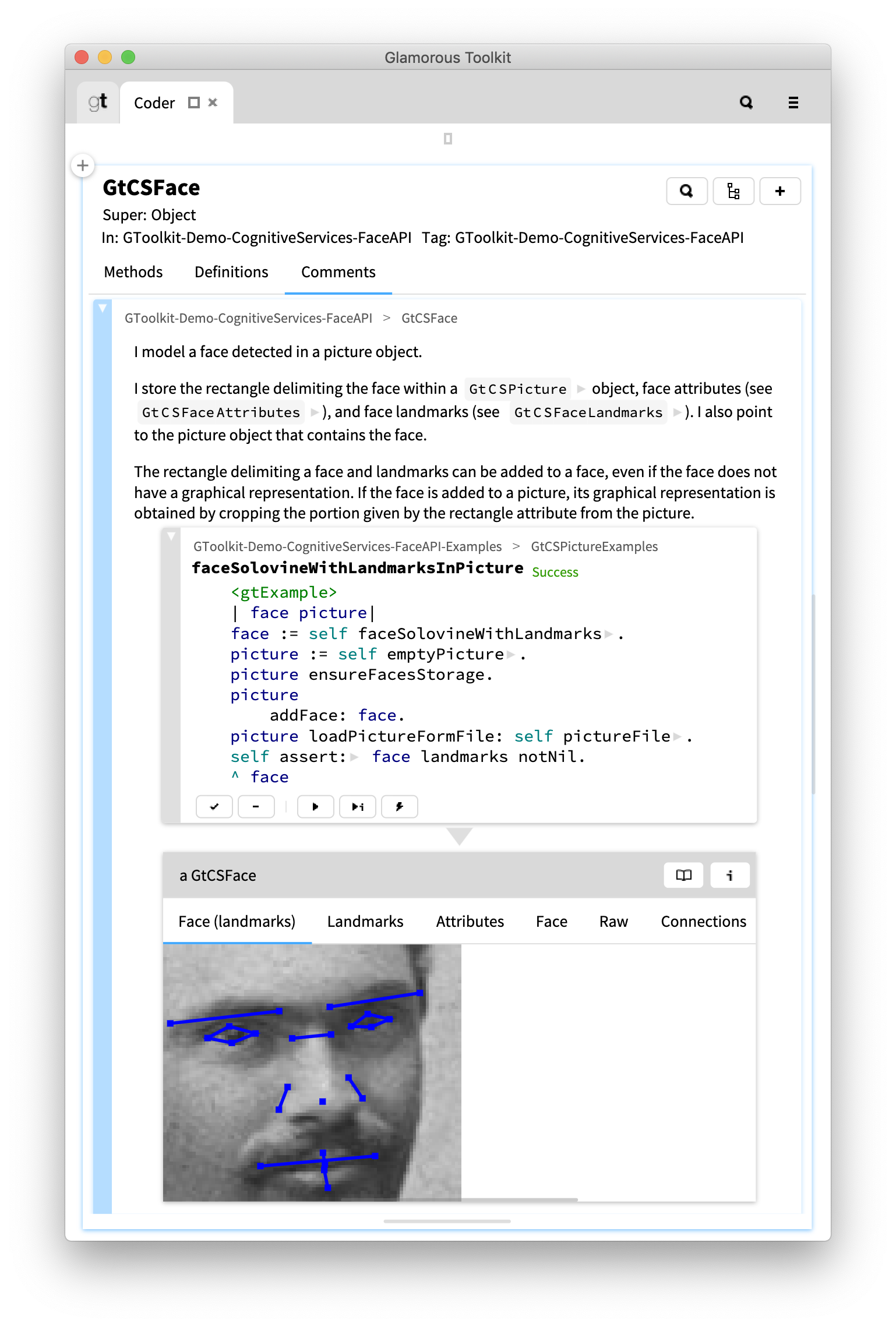
Example methods from a code comment can be directly executed when looking at the code comment.

The inspector in Glamorous Toolkit allows every object to have multiple custom views. Executing an example embeds in the editor an inspector on the resulting object. This enables us to use views as part of documentation.

For example, Face objects have a view showing how landmarks map onto the face that we can embed in the comment. Hence, our documentation does no longer have to consist only in static text or pictures. It can rely on live views created while a reader is interacting with the comment.

Examples also contain assertions. These are checked every time we run an example. Above we can see the green ‘Success’ label after the method name, indicating that all assertions passed. By running examples as part of our CI pipelines we can be a bit more confident that our documentation is up to date.

Embedding views

Often showing more graphical content in a code comment can be useful.

Let us consider that in our example comment we would find it useful to place, after the second paragraph, a graphical representation of a face containing landmarks. One way would be to create an image with this information that we would then load, from disk or from an URL, and show in the comment.

Another alternative consists in expressing that graphical representation as a view of an object, writing an example method creating the necessary object, and embedding the resulting view in the comment.

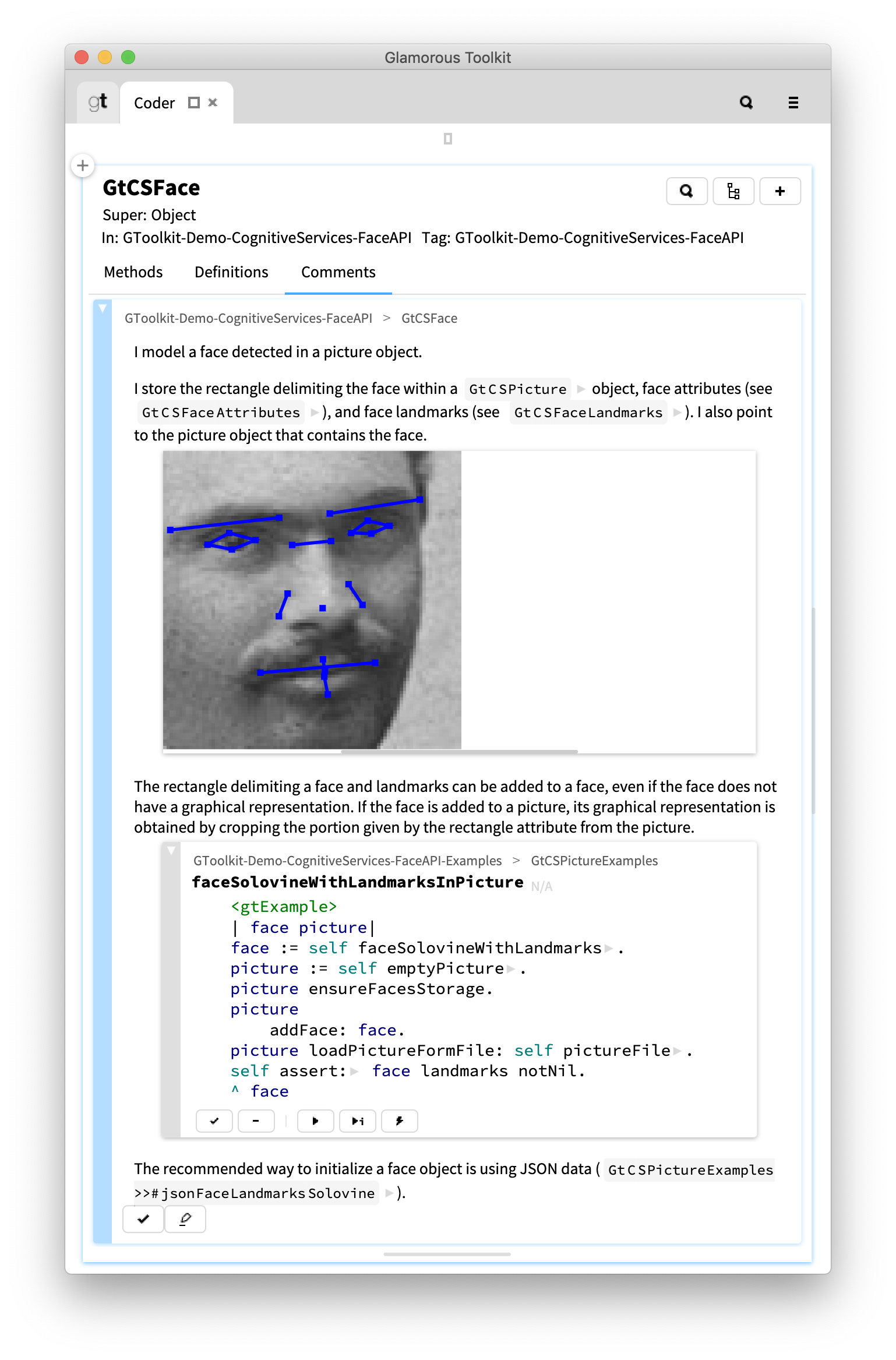
Code comments can further embed live views for objects.

When executing an example we might not want to always show the entire inspector. Sometimes a single view is better. In our comment, the third paragraph talks about adding landmarks to faces that do not have a graphical representation. To show this we can write a dedicated example creating such a face object, and embed just the view showing landmarks.

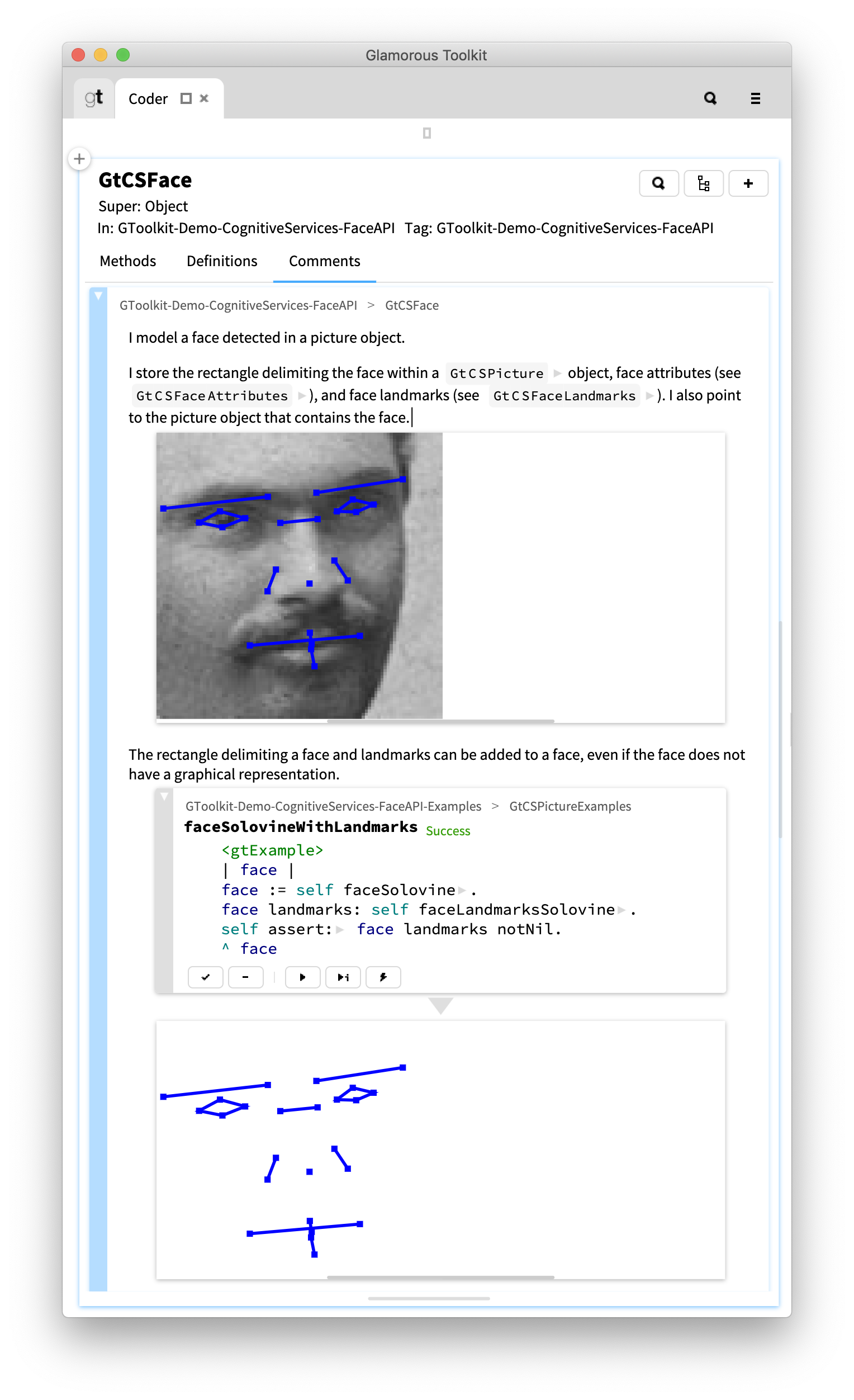
The creator of a comment can decide to show a specific view when a reader executes an example method.

Now we have a story in our code comment. The initial view introduces a face with landmarks. Next we see the code to attach landmarks to a face, together with a view showing the positioning of those landmarks. At the end we get the complete code to create a face with landmarks and a graphical representation. We also get a full-fledged object inspector to further explore that object.

A look under the hood

Above we only see how the comment looks like, but not how the creator of the comment embeds views, or examples into the comment.

Documenter relies on a markup language (i.e., Pillar. Example methods and other artefacts are embedded through various annotations. For example the following example annotation embeds the code of the example method faceSolovineWithLandmarks.

` ${example:GtCSPictureExamples>>#faceSolovineWithLandmarks}$ `

We can see and edit these annotations directly in the comment by going with the cursor at the beginning of a line showing a view, editor or link. Below we see the annotation for embedding the view showing a face with landmarks.

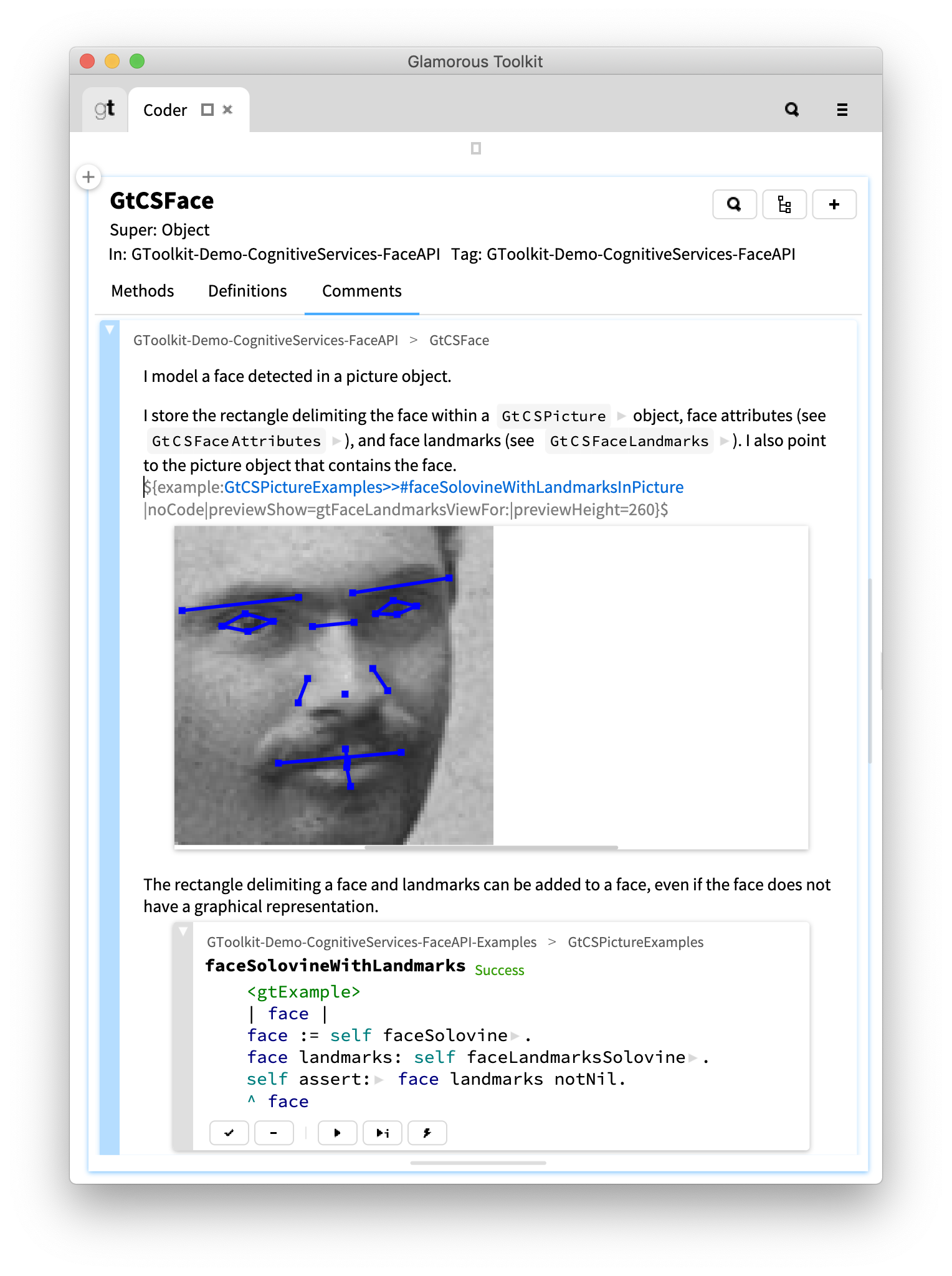
Annotations are shown and can be changed when the cursor is placed near links, views or editors.

Hence, comments are still created and shared as text. However, they are no longer consumed as static text documents.

Enabling exploration

Understanding a software system is an activity that entails navigation through a web of interconnected code, run-time objects and data.

Diving into code

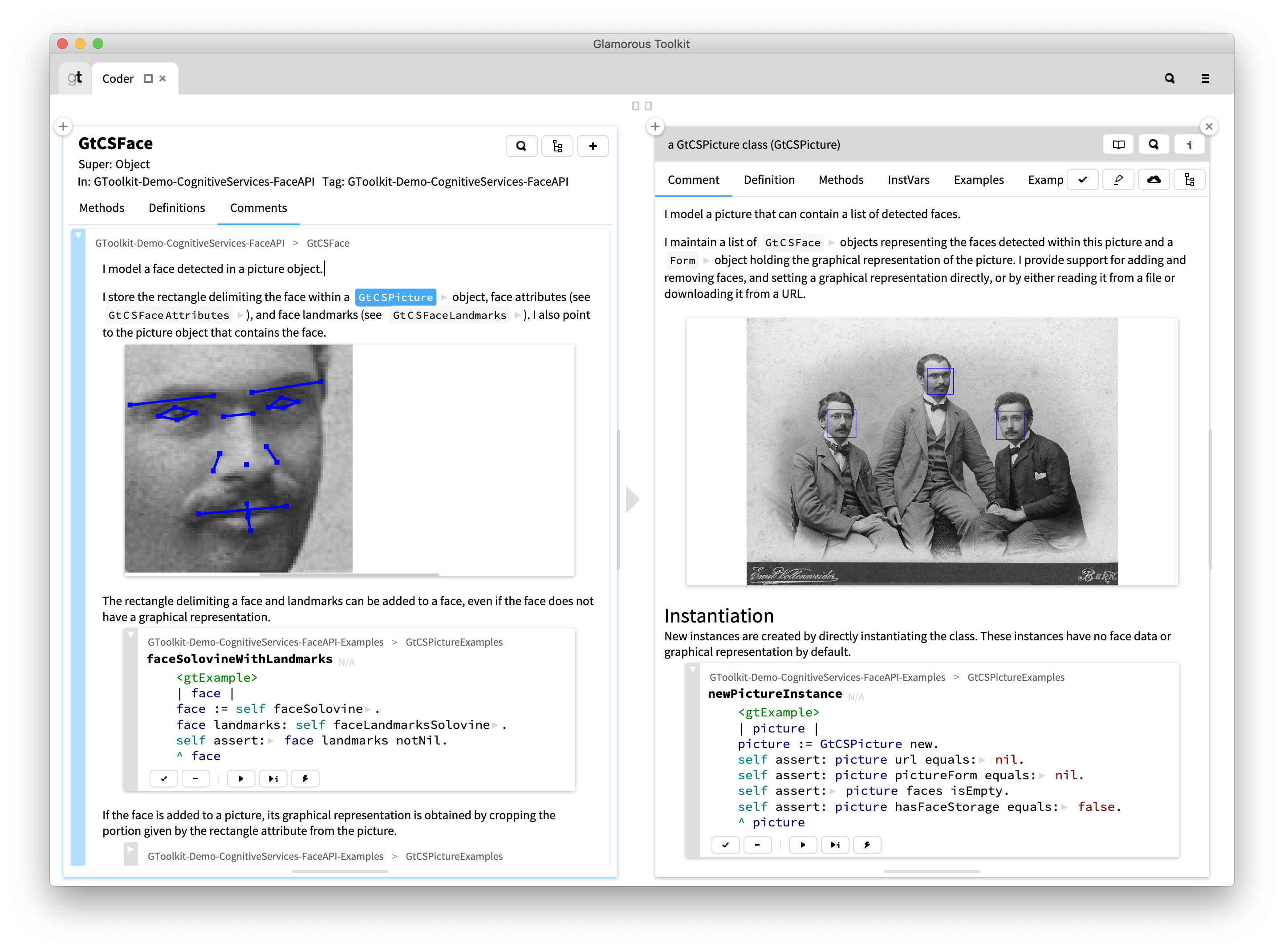
From a code comment a developer can navigate to any code entity referenced in that comment. All code entities referenced in a comment are by default buttons and open that entity in a new page to the right. For example, below, we start with the Face class and navigate to the Picture class.

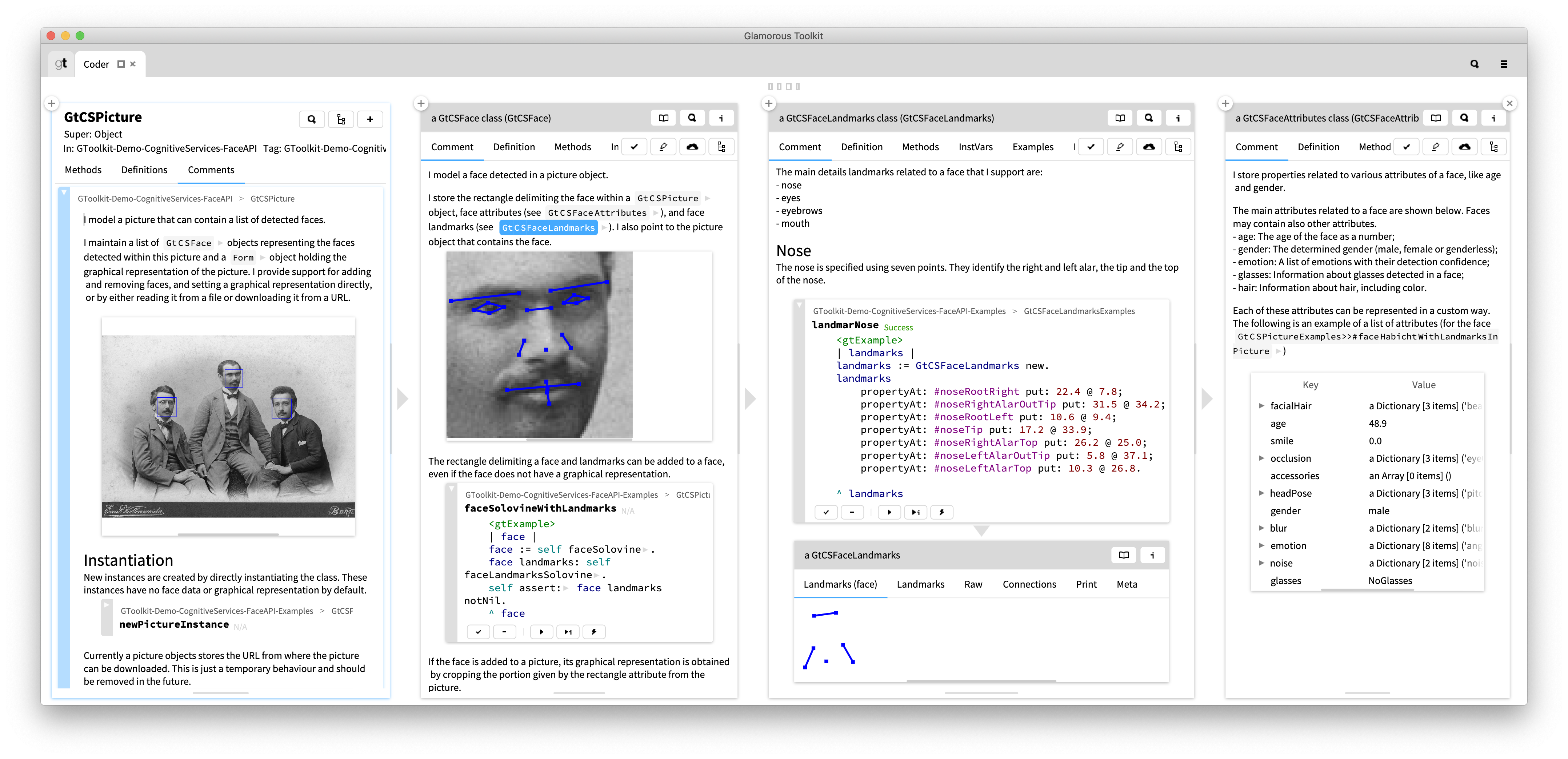
Explorations do not have to be limited to one single page. From the new page the developer can further continue the navigation. Below, the developer starts by looking at the Picture class, dives into the Face class, continues by exploring face landmarks and finally face attributes.

We do not have to limit our navigation to a single code entity.

Diving into objects

Not only diving into code is needed. Sometimes, continuing the exploration by investigating an object can provide better insights. From a document, whenever an example is embedded in the document, the reader can continue the navigation by diving into that example.

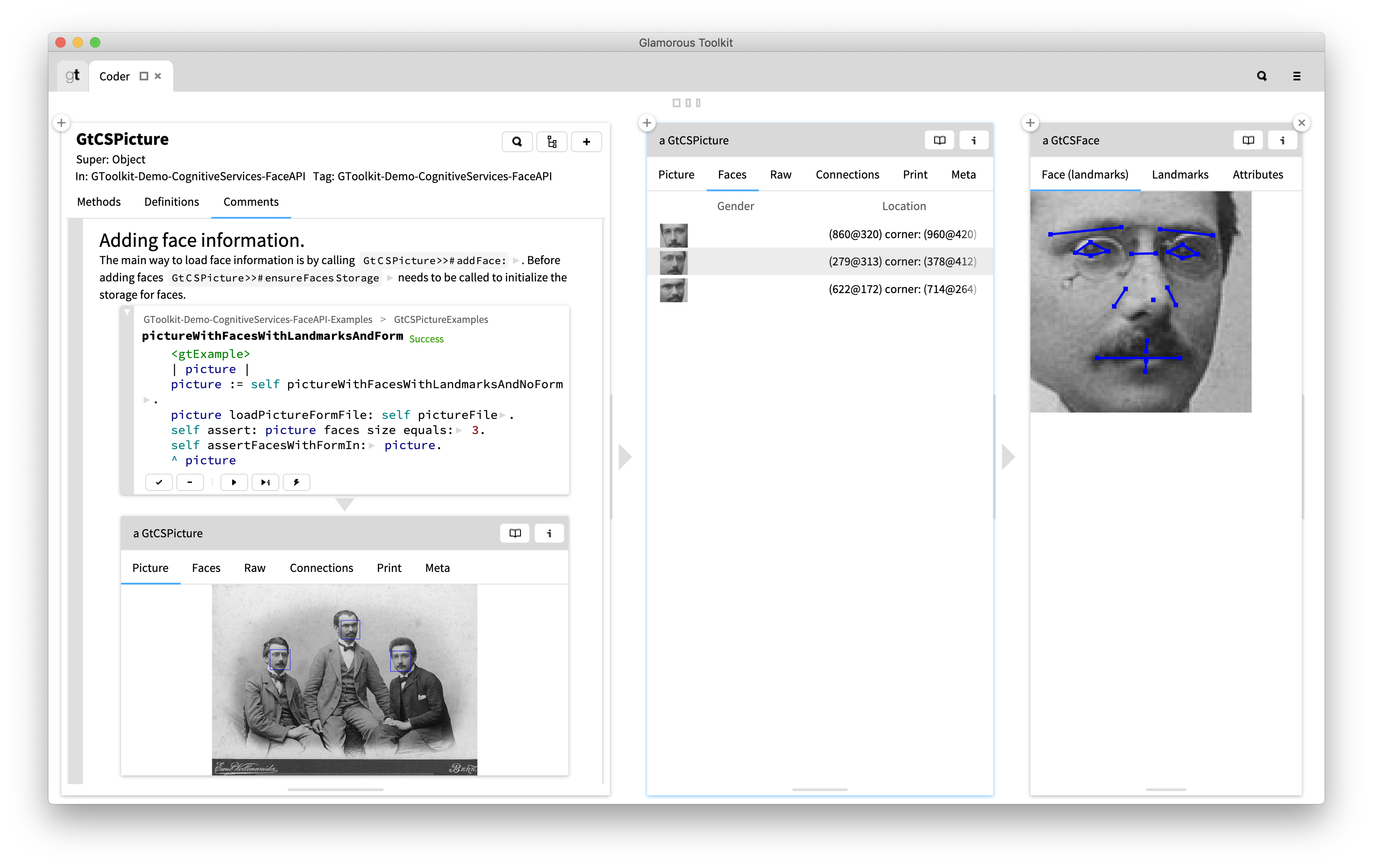
Diving into an example object embedded in a code comment. Developers can further dive into the internals of that object.

As with code, explorations are not limited to a single page. The developer can continue for as long as needed. Explorations are also not limited to only code entities, or only objects. Both can be seamlessly intertwined.

A navigation session can intertwine objects and code entities.

Wrap-up

Writing code comments is a tedious activity. Alongside it we often do other activities like testing and building tools to explore and visualise our systems. These are often seen as activities independent of one another. However, that does not have to be the case. The effort to write tests and build tools for our systems can be reused to improve the way we create documentation.

With Documenter if we structure our tests as examples we can directly embed them in our code comments and allow readers to interact with them. As examples return objects we can start from those objects, take inspector views that show them in interesting ways and embed them in comments. Each code comment becomes a live notebook.

Once we have a comment we can link it to other relevant code entities and objects, and enable readers to navigate through them. Comments become a live wiki where we can seamlessly navigate through code and objects.

feenk blog